MoE means the mixture of expert. In this blog, we will introduce the type of MoE used in the mixtral8x7B model. The blog will assume that you already understand the llama2 model. Thus, we will not revisit any knowledge already inside the llama2 model. Another focus of this blog will combine the code implementation to delve into the arc of MoE.
Difference from the llama2
In causal LM, we know that the decoder model can be decomposed into multiple small parts. Let’s visit the architecture of the llama2 in the Figure 1.
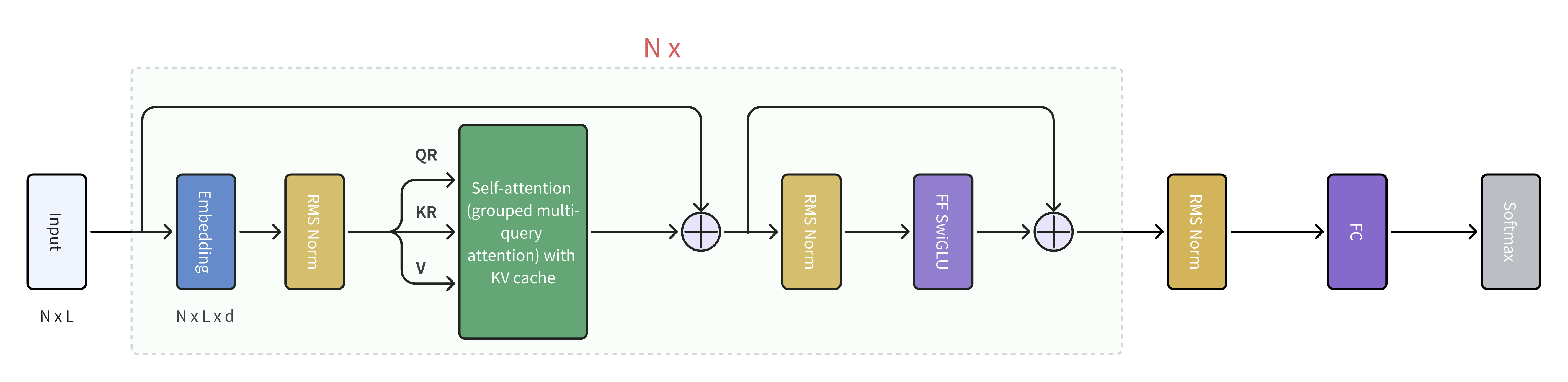
There are many components inside the llama2 architecure, like the attention layer, positional embedding, RMS norm, FC etc. The only difference here is the block of FF SwiGLU (FF is the feedforward network and the implementation is add the hidden embedding dimension first, through the activation function and finally decrease the dimension). Instead of using only one FF function, we use the mixture of expert, which export is the actually a FF. In llama2, the code implementation would be as simple as:
class LlamaMLP(nn.Module):
def __init__(self, config):
super().__init__()
self.config = config
self.hidden_size = config.hidden_size
self.intermediate_size = config.intermediate_size
self.gate_proj = nn.Linear(self.hidden_size, self.intermediate_size, bias=False)
self.up_proj = nn.Linear(self.hidden_size, self.intermediate_size, bias=False)
self.down_proj = nn.Linear(self.intermediate_size, self.hidden_size, bias=False)
self.act_fn = ACT2FN[config.hidden_act]
def forward(self, x):
down_proj = self.down_proj(self.act_fn(self.gate_proj(x)) * self.up_proj(x))
return down_projOK, now we will add more complexity to this function. ::: {.callout-tip} Note that all other parts are the same except the feedforward block. :::
Mathematical insights
The FF model is actually the expert! For the llama2 model, we only have one expert, therefore, in the case of llama2, we have
\[ y = E(x), \]
where \(x, y\) are the value before and after the FF block. In the MoE, we actually prepare multiple trainable experts, so there are multiple E layers. A gating network is thus introduced to decide which network should be used. And now the expression becomes:
\[ y = \sum_{i=1}^n G(x)_i E_i(x). \]
It is special to choose the network G. Here, we just introduce the found research work from the paper Switch Transformer which is also the famous Mixtral-8x7B.
Specially for this model, n=8. Suppose the last dimension of x is d, we will include the dimension of each variables for following up explanation.
The steps to construct the G(x) are:
- Set trainable linear layer \(W_g\) of size
d*n. \[ H(x)= x \cdot W_{\mathrm{g}} \] and we know the dimension of \(H(x)\) is \(n=8\). - Only pick the top K experts: \[ \operatorname{KeepTopK}(v, k)_i= \begin{cases}v_i & \text { if } v_i \text { is in the top } k \text { elements of } v \\ -\infty & \text { otherwise. }\end{cases} \]
- Apply the softmax to get the final
G(x)\[ G(x)=\operatorname{Norm}(\operatorname{Softmax}(\operatorname{KeepTopK}(H(x), k))) \]
Set to \(-\infty\) so that it becomes zero during softmax. Thus, for the final output, we only have \(k\) experts which are really used.
For different tokens (tokens in the same sequence and batch could be routed to different experts), they will choose different experts! For example the batch[0] will choose the expert 0 and 3, while the batch[1] will choose the expert 4 and 7.
Load balancing loss
Since different portion of total tokens will enter different experts, like the unbalanced dataset problem, we need to add a load balancing loss. Given \(N\) experts indexed by \(i=1\) to \(N\) and a batch \(\mathcal{B}\) with \(T\) tokens, the auxiliary loss is computed as the scaled dot-product between vectors \(f\) and \(P\), \[ \text { loss }=\alpha \cdot N \cdot \sum_{i=1}^N f_i \cdot P_i \] where \(f_i\) is the fraction of tokens dispatched to expert \(i\), \[ f_i=\frac{1}{T} \sum_{x \in \mathcal{B}} \mathbb{1}\{\operatorname{argmax} p(x)=i\} \] and \(P_i\) is the fraction of the router probability allocated for expert \(i,{ }^2\) \[ P_i=\frac{1}{T} \sum_{x \in \mathcal{B}} p_i(x) \]
We add this loss since we want to encourages uniform routing since the loss is minimized when \[ f_i = P_i = \frac{1}{N}. \]
Theorem 1 To prove that the minimum of the objective function \(\mathbf{a} \cdot \mathbf{b}=\sum_{i=1}^N a_i b_i\) is achieved when \(a_i=\) \(b_i=\frac{1}{N}\) under the given constraints, we use the method of Lagrange multipliers for the constraints:
Given constraints:
- \(\sum_{i=1}^N a_i=1, a_i \geq 0\).
- \(\sum_{i=1}^N b_i=1, b_i \geq 0\).
Objective Function to minimize:
- \(L=\mathbf{a} \cdot \mathbf{b}-\lambda\left(\sum_{i=1}^N a_i-1\right)-\mu\left(\sum_{i=1}^N b_i-1\right)\), where \(\lambda\) and \(\mu\) are Lagrange multipliers.
Taking partial derivatives of \(L\) with respect to \(a_i, b_i, \lambda\), and \(\mu\) and setting them to zero gives:
- \(\frac{\partial L}{\partial a_i}=b_i-\lambda=0 \Rightarrow b_i=\lambda\).
- \(\frac{\partial L}{\partial b_i}=a_i-\mu=0 \Rightarrow a_i=\mu\).
- \(\frac{\partial L}{\partial \lambda}=\sum_{i=1}^N a_i-1=0\).
- \(\frac{\partial L}{\partial \mu}=\sum_{i=1}^N b_i-1=0\).
From equations 1 and 2 , all \(a_i\) and \(b_i\) must be constant for all \(i\), because they equal the respective Lagrange multipliers \(\lambda\) and \(\mu\), which are constants. Thus, \(a_i=a\) and \(b_i=b\) for some constants \(a\) and \(b\) for all \(i\).
Given the constraints \(\sum_{i=1}^N a_i=1\) and \(\sum_{i=1}^N b_i=1\), and knowing that \(a_i=a\) and \(b_i=b\) for all \(i\), we have:
- \(\sum_{i=1}^N a=N \cdot a=1 \Rightarrow a=\frac{1}{N}\).
- \(\sum_{i=1}^N b=N \cdot b=1 \Rightarrow b=\frac{1}{N}\).
Therefore, setting \(a_i=b_i=\frac{1}{N}\) for all \(i\) satisfies the constraints and minimizes the objective function \(\mathbf{a} \cdot \mathbf{b}=\sum_{i=1}^N a_i b_i\), as any local minimum in a convex function over a convex set is a global minimum.